valor absoluto: El Valor Absoluto se define como la distancia entre dos números
reales en la recta numérica. Con el objeto de afianzar el concepto de valor absoluto, es necesario
ligarlo a su interpretación geométrica en la recta numérica.
Para realizar este trabajo usted deberá estudiar previamente la sección 6.2 del libro
Precálculo Una Nueva Visión, G.Mora – M.M.Rey – B.C. Robles, Editorial Escuela
Colombiana de Ingeniería, Edición Preliminar Tercera Versión y hacer los ejercicios de
la sección 6.1
Ejemplo
Comparar las distancias entre un número real cualquiera y los puntos –6 y 4
Al observar la recta numérica se tiene que los puntos –6 y 4 la dividen en tres grandes intervalos
( −∞,−6) ,[−6 4, ] y ( 4,∞ )
( −∞,−6) [ −6 4, ] ( 4,∞ )
∀ ∈x ( −∞,−6) se tiene:
La distancia de cualquier punto
x al punto –6 es menor que su
distancia a 4, lo que en
términos de valor absoluto se
puede expresar así:
x x − −( ) 6 4 < − ⇔
x x + < 6 4 −
∀ x ∈ −[ 6 4, ] se tiene:
a. El punto medio entre –6 y 4
es –1, por lo tanto al ubicar el
punto x en –1 la distancia
entre –6 y x es igual que la
distancia entre x y 4, lo que
puede escribirse en términos
de valor absoluto como:
x x − ( ) − = 6 4 − ⇔
x x + 6 4 = −
b. Si x está más cerca de –6
que de 4, se tiene:
x x − ( − < 6 4 ) − ⇔
x x + 6 4 < −
c. Si x está más lejos de –6 que
de 4, se tiene:
x x − ( − > 6 4 ) − ⇔x x + 6 4
valor absoluto (o módulo) | a | de un número real a es el valor numérico de una sin tener en cuenta su signo .Así, por ejemplo, el valor absoluto de 3 es 3, y el valor absoluto de -3 es también 3. El valor absoluto de un número puede ser pensado como su distancia de cero.
Definición y propiedades
[ editar ]Los números reales
Para cualquier
número real un valor absoluto o el
módulo de A se denota por
| a | (una
barra vertical en cada lado de la cantidad) y se define como
[6]
Como puede verse a partir de la definición anterior, el valor absoluto de
a es siempre sea
positivo o
cero , pero nunca
negativo .
De una
geometría analítica punto de vista, el valor absoluto de un número real es que el número de
distancia de cero a lo largo de la
línea número real , y más en general el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, la noción de un extracto
función de distancia en matemáticas puede ser visto como una generalización del valor absoluto de la diferencia (ver
"Distancia" a continuación).
Desde la
raíz cuadrada notación sin signo representa la raíz cuadrada
positiva, se sigue que
 | ( 1 ) |
que se utiliza a veces como una definición de valor absoluto.
[7]
El valor absoluto tiene las siguientes cuatro propiedades fundamentales:
-
Otras propiedades importantes del valor absoluto incluyen:
-
Dos otras propiedades útiles referentes a las desigualdades son:

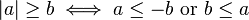
Estas relaciones pueden ser utilizados para resolver las desigualdades de valores absolutos. Por ejemplo:
-
Valor absoluto se usa para definir la
diferencia absoluta , la métrica estándar en los números reales.
[ editar ]Los números complejos

El valor absoluto de un número complejo
zes la distancia
r desde el origen a
z.También se ve en la imagen que
z y su
complejo conjugado de z tiene el mismo valor absoluto.
Dado que los
números complejos no están
ordenados , la definición dada anteriormente para el valor absoluto real no puede ser directamente generalizada de un número complejo. Sin embargo, la interpretación geométrica del valor absoluto de un número real como su distancia de 0 puede ser generalizada. El valor absoluto de un número complejo se define como su distancia en el
plano complejo de la
origen usando el
teorema de Pitágoras . Más en general el valor absoluto de la diferencia de dos números complejos es igual a la distancia entre esos dos números complejos.
Para cualquier número complejo

donde x e y son números reales, el valor absoluto o módulo de z se denota | z | y está dada por

Cuando la parte compleja y es cero, esto es el mismo que el valor absoluto del número realx.
Cuando un número complejo
z se expresa en
forma polar como
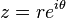
con r ≥ 0 y θ reales, su valor absoluto es
 .
.
El valor absoluto de un número complejo se puede escribir en el complejo análogo de la ecuación
(1) anterior como:

El valor absoluto complejo comparte todas las propiedades del valor absoluto real dada en las ecuaciones (2) - (11) anteriormente.
Dado que los reales positivos forman un subgrupo de los números complejos bajo multiplicación, podemos pensar en valor absoluto como un
endomorfismo del
grupo multiplicativo de los números complejos.
Función valor absoluto
La verdadera función valor absoluto es
continua en todas partes. Es
diferenciable en todas partes excepto en
x = 0. Se
monótonamente decreciente en el intervalo
(- ∞, 0] y monótonamente creciente en el intervalo
[0, + ∞). Dado un número real y su negativa tiene el mismo valor absoluto, es una
función par , y por lo tanto no es
invertible .
 o
o  se denomina inecuación en sentido estricto y si es del tipo
se denomina inecuación en sentido estricto y si es del tipo  o
o  se denomina inecuación en sentido amplio.[3]
se denomina inecuación en sentido amplio.[3] o
o  se denomina inecuación en sentido estricto y si es del tipo
se denomina inecuación en sentido estricto y si es del tipo  o
o  se denomina inecuación en sentido amplio.[3]
se denomina inecuación en sentido amplio.[3] .
. .
. .
. .
. .
. .
. .
. .
.





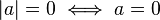




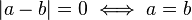
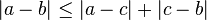



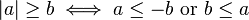






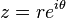
 .
.
 es el
es el
Inecuaciones de primer grado
Son aquellas en las que la incognita está elevada a 1, como 2x - 3 < x + 5
Sus soluciones pueden ser de uno de estos cuatro tipos:
x < a x > a x =< a x >= a * (infinito)
X E (- * , a) X E (a , + *) X E ( - * , a) X E (a, + *)
Inecuaciones polinómicas de grado superior y racionalesSon aquellas en las que la incognita forma parte de un polinomio de grado mayor que 1 (polinómicas) o de una fraccion algebraica (racionales).
Inecuaciones polinómicas
x^2 - 5x + 6 > 0 => (x-2) (x-3) > 0
Inecuaciones racionales
x - 1
------- =< 0
x + 2